Model Selection Problem
There are so many models learned, even just for binary classification :
$$A\epsilon \{PLA,\ pocket,\ linear\ regression,\ logistic\ regression\}\times$$
$$T\epsilon \{100, 1000, 1000\}\times$$
$$\eta\epsilon\{1,0.01,0.0001\}\times$$
$$\phi\epsilon\{linear,\ quadratic,\ poly-10,\ Legendre-poly-10\}\times$$
$$\Omega(w)\epsilon\{L2\ regularizer,\ L1\ regularizer,\ symmetry\ regularizer\}\times$$
$$\lambda\epsilon\{0,0.01,1\}$$
- given : $M$ models $H_1,H_2,…,H_M$ , each with corresponding algorithm $A_1,A_2,…,A_M$
- goal : select $H_{m^}$ such that $g_{m^}=A_{m^}(D)$ is of low $E_{out}(g_{m^})$
- unknown $E_{out}$ due to unknown $P(x) and P(y|x)$ , as always
- arguably the most important practical problem of ML .
1. Model Selection by Best $E_{in}$
$$m^*=\mathop{argmin}\limits_{1\leq m\leq M}(E_m=E_{in}(A_m(D)))$$
BUT :
- $\phi_{1126}$ always more preferred over $\phi_1$ and $\lambda=0$ always more preferred over $\lambda=0.1$
- if $A_1$ minimizes $E_{in}$ over $H_1$ and $A_2$ minimizes $E_{in}$ over $H_2$ ,
$\Rightarrow g_{m^*}$ achieves minimal $E_{in}$ over $H_1 \cup H_2$
$\Rightarrow$ ‘model selection + learning’ pays $d_{vc}(H_1 \cup H_2)$
—> bad generalization .
2. Model Selection by Best $E_{test}$
$$m^*=\mathop{argmin}\limits_{1\leq m\leq M}(E_m=E_{test}(A_m(D)))$$
Generalization Guarantee :
$$E_{out}(g_{m^*})\leq E_{test}(g_{m^*})+O(\sqrt{\frac{log\ M}{N_{test}}})$$
BUT :
where is $D_{test}$ —> selecting by $E_{test}$ is infeasible and cheating .
3. Comparison between $E_{in}$ and $E_{test}$
As $E_{in}$ not workable and $E_{test}$ infeasible , we find something in between : $E_{val}$
$E_{val}$ was calculated from $D_{val}\subset D$ , feasible on hand , ‘clean’ if $D_{val}$ never used by $A_m$ before .
Validation
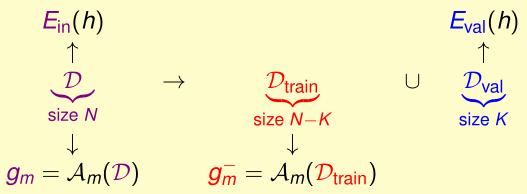
$$E_{out}(g_m^-)\leq E_{val}(g_m^-)+O(\sqrt{\frac{log\ M}{K}})$$
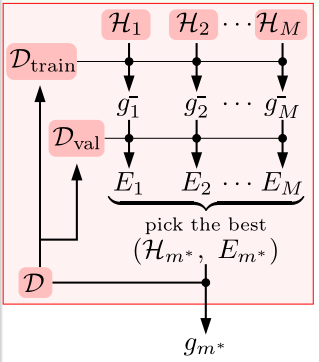
$$m^*=\mathop{argmin}\limits_{1\leq m\leq M}(E_m=E_{val}(A_m(D_{train})))$$
$$E_{out}(g_{m^*})\leq E_{out}(g_m^-)\leq E_{val}(g_m^-)+O(\sqrt{\frac{log\ M}{K}})$$
- in-sample : selection with $E_{in}$
- optimal : cheating-selection with $E_{test}$
- $g_{m^*}^-$ : selection with $E_{val}$ and report $g_{m^*}^-$
- $g_{m^*}$ : selection with $E_{val}$ and report $g_{m^*}$
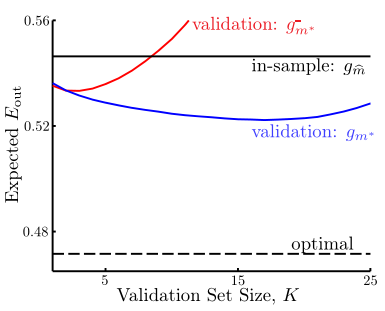
The Dilemma about K
- large K : every $E_{val}\approx E_{out}$ , but all $g_m^-$ much worse than $g_m$
- small K : every $g_m^-\approx g_m$ , but $E_{val}$ far from $E_{out}$
practical rule of thumb : $K=\frac N5$
Leave-One-Out Cross Validation
Extreme case : take K = 1 , $D_{val}^{(n)}=\{(x_n,y_n)\}\ and\ E_{val}^{(n)}(g_n^-)=err(g_n^-(x_n),y_n)=e_n$
leave-one-out cross validation estimate :
$$E_{loocv}(H,A)=\frac 1N\sum_{n=1}^Ne_n=\frac 1N\sum_{n=1}^Nerr(g_n^-(x_n),y_n)$$
hope : $E_{loocv}(H,A)\approx E_{out}(g)$
Theoretical Guarantee of Leave-One-Out Estimate
$$\varepsilon_D\ E_{loocv}(H,A)=\varepsilon_D\ \frac 1N\sum_{n=1}^Ne_n=\frac 1N\sum_{n=1}^N\varepsilon_{D_n}\varepsilon_{(x_n,y_n)}err(g_n^-(x_n),y_n)=\frac 1N\sum_{n=1}^N\varepsilon_{D_n}E_{out}(g_n^-)=\bar{E_{out}}(N-1)$$
V-Fold Cross Validation
Disadvantages of Leave-One-Out Estimate
- computation : N ‘additional’ training per model , not always feasible in practice .
- stability : due to variance of single-point estimates .
$E_{loocv}$ not often used practically
V-Fold Cross Validation
random-partition of $D$ to $V$ equal parts , take $V-1$ for training and $1$ for validation orderly .
5-Fold or 10-Fold generally works well .
Nature of Validation
- all training models : select among hypothesis .
- all validation schemes : select among finalists .
- all testing methods : just evalute .
Do not fool yourself , report test result , not best validation result .