Regularization Hypothesis Set

idea : ‘step back’ from $H_{10}$ to $H_2$

E.g.
hypothesis $w$ in $H_{10}$ : $w_0+w_1x+w_2x^2+…+w_{10}x^{10}$
hypothesis $w$ in $H_2$ : $w_0+w_1x+w_2x^2$
that is, $H_2=H_{10}$ AND ‘constraint that $w_3=w_4=…=w_{10}=0$ ‘ .

即通过 constraint 减小假设空间，后面会提到这也某种程度上降低了 $d_{vc}$ ，从而降低模型的复杂度，进而起到减缓过拟合的作用 .

下面以回归任务的 error function 为例分析如何设计 constraint ($L_2$) ，当然后面我们会看到分析过程并不依赖于具体的 error function ，所以只要合适，我们也可以将 $L_2$ 用于 Logistic regression 中 .

首先我们将条件 $w_3=w_4=…=w_{10}=0$ 放宽到不为0的最多三个，也就是在回归问题中我们要求解：
$$\mathop{min}\limits_{w\epsilon \mathbb{R}^{10+1}}E_{in}(w)\qquad s.t.\sum\limits_{q=0}^{10}[w_q\neq 0]\leq 3$$
more flexible than $H_2$ ($H_2\subset H_2^{‘}$) & lesss risky than $H_{10}$ ($H_2^{‘}\subset H_{10}$)
但是对于求解这样的问题是 NP-hard 的 .

我们进一步放宽条件，使得 $w$ 不会太大，即求解这样的问题：
$$\mathop{min}\limits_{w\epsilon \mathbb{R}^{10+1}}E_{in}(w)\qquad s.t.\sum\limits_{q=0}^{10}w_q^2\leq C$$
$H(C)$ : overlaps but not exactly the same as $H_2^{‘}$
soft and smooth structure over $C\geq 0$ :
$$H(0)\subset H(1.126)\subset …\subset H(1126)\subset…\subset H(\infty)$$

再接下来就是从这样的正规化过的假设空间 $H(C)$ 中找到最优解 .

Weight Decay Regularization

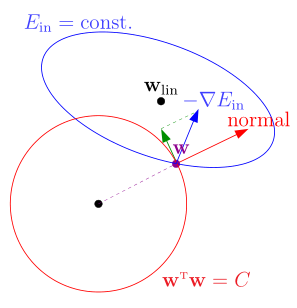
$$\mathop{min}\limits_{w\epsilon \mathbb{R}^{Q+1}} E_{in}(w)=\frac{1}{N}(Zw-y)^T(Zw-y)\ \ s.t. w^Tw\leq C$$

$w$ 通常会出现在红圈的边缘上，更新的方向还是梯度相反方向 $-\bigtriangledown E_{in}(w)$ . 如果 $-\bigtriangledown E_{in}(w)$ 与 $w$ 不平行的话，我们就需要向梯度反向在 $w$ 垂直的方向上的投影方向上更新，一直到这两者平行 .

want: find Lagrange multiplier $\lambda >0$ and $w_{REG}$ such that $\bigtriangledown E_{in}(w_{REG})+\frac {2\lambda}{N}w_{REG}=0$
try to solve the Equation by substituting $\bigtriangledown E_{in}(w_{REG})$ :
$$\frac {2}{N}(Z^TZw_{REG}-Z^TY)+\frac {2\lambda}{N}w_{WEG}=0$$
optimal solution :
$$w_{REG}\leftarrow (Z^TZ+\lambda I)^{-1}Z^TY$$
if we have $\lambda\geq0$ , then we have closed-form solution .

Augmented Error
Actually, solving $$\bigtriangledown E_{in}(w_{REG})+\frac {2\lambda}{N}w_{REG}=0$$ equivalent to minimizing $$E_{in}(w)+\frac{\lambda}{N}w^Tw$$ regularization with augmented error instead of constrained $E_{in}$ $$w_{REG}\leftarrow \mathop{argmin}\limits_wE_{aug}(w)\ for\ given\ \lambda\geq0$$
minimizing unconstrained $E_{aug}$ effectively minimizes some C-constrained $E_{in}$

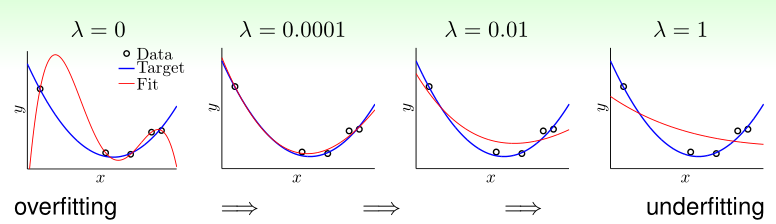
E.g.

philosophy: a little regularization goes a long way !

call ‘$+\frac\lambda Nw^Tw$’ weighted-decay regularization :
larger $\lambda$ $\Leftrightarrow$ prefer shorter $w$ $\Leftrightarrow$ effectively smaller C
—>go with ‘any’ transform + linear model .

Legendre Polynomials
For naive polynomial transform :
$$\Phi(x)=(1,x,x^2,…,x^Q)$$
when $x_n\epsilon[-1,+1]$ , $x_n^Q$ really small, needing larger $w_q$ .
Use normalized polynomial transform :
$$(1, L_1(x), L_2(x), … , L_Q(x))$$
‘orthonormal basis functions’ called Legendre Polynomials .
E.g.

Regularization and VC Theory

Augmented Error : $E_{aug}(w)=E_{in}(w)+\frac{\lambda}{N}w^Tw$
VC Bound : $\qquad\ \ E_{out}(w)\leq E_{in}(w)+\Omega(H)$

regularizer $w^w$ : complexity of a single hypothesis
generalization price $\Omega(H)$ : complexity of a hypothesis set
if $\frac\lambda N\Omega(w)$ ‘represents’ $\Omega(H)$ well, $E_{aug}$ is a better proxy of $E_{out}$ than $E_{in}$ .

Effective VC Dimension
$$\mathop{min}\limits_{w\epsilon \mathbb{R}^{d+1}}E_{aug}(w)=E_{in}(w)+\frac \lambda N\Omega(w)$$
model complexity : $d_{vc}(H)=d+1$, because {$w$} ‘all considered’ during minimization
{$w$} ‘actually needed’ : $H(C)$, with some $C$ equivalent to $\lambda$
$d_{vc}(H(C))$ : effective VC dimension $d_{EFF}(H, A)$

explanation of regularization :
$d_{vc}(H)$ large, while $d_{EFF}(H,A)$ small if $A$ regularized .

General Regularizers

want : constraint in the ‘direction’ of target function .

target-depedent : some properties of target, if known . E.g. symmetry regularizer : $\sum[q\ is\ odd]w_q^2$
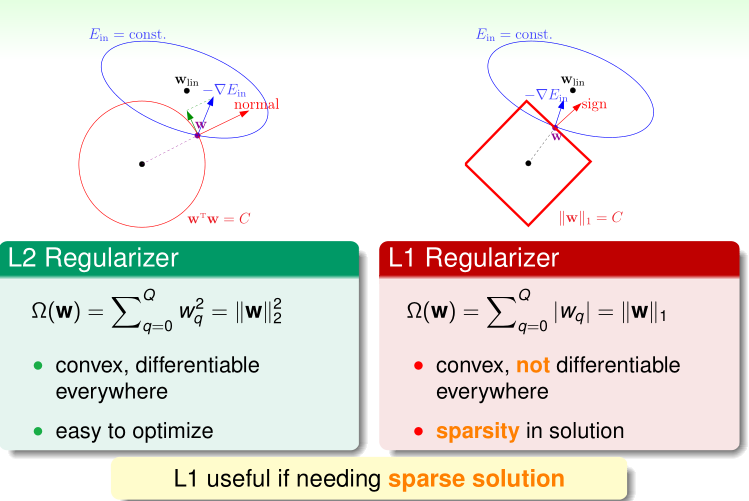
plausible ; direction towards smoother or simpler . E.g. sparsity (L1) regularizer : $\sum|w_q|$
friendly : easy to optimize . E.g. weight-decay (L2) regularizer : $\sum w_q^2$

augmented error = error $\hat{err}$ + regularizer $\Omega$ .

L1 VS. L2

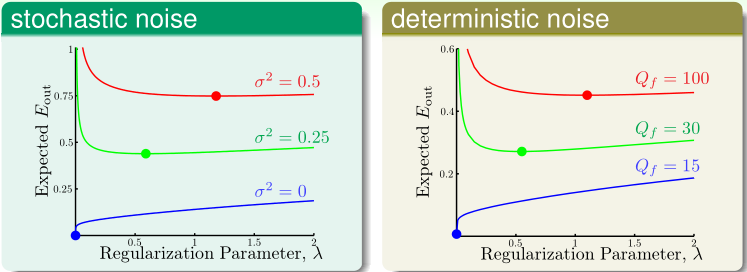
The optimal $\lambda$

more noise $\Leftrightarrow$ more regularization needed
noise unknown —> important to make proper choices .