Quadratic Hypotheses

有时候在某些 $D$ 上总会出现所有的 lines $E_{in}$ 都很大，这种时候线性假设就存在表达限制. 但是也许是 circular separable 的，例如对于假设 $h(x)=sign(-x_1^2-x_2^2+0.6)$ 如何将线性的一些求解算法应用到这种二次可分的假设上呢？

这里我们可以把 $x_1^2$ 等作为整体 $z_1$ 来看待，这样就映射到了熟悉的线性中的情况.

$\{(x_n,y_n)\}\ circular\ separable\ \Rightarrow\ \{(z_n,y_n)\}\ linear\ separable$
$x\epsilon X\ \mathop{\mapsto}\limits^{\Phi}\ z\epsilon Z\ with\ nonlinear\ feature\ transform\ \Phi$

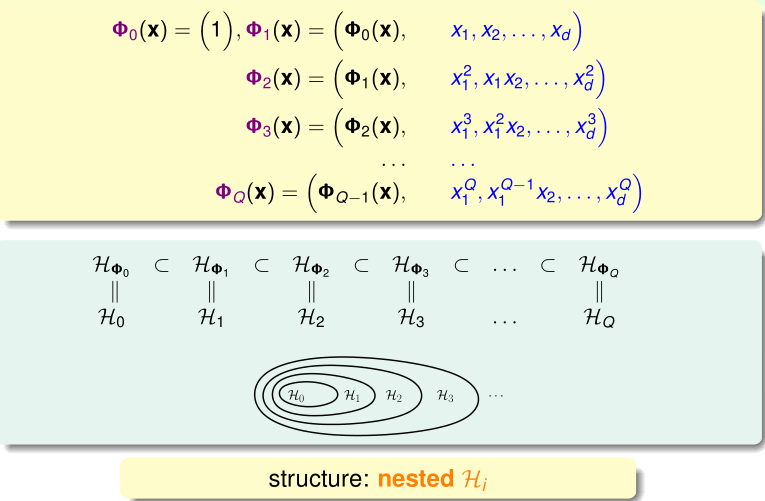
对于二次的情况，我们可以使用一个更大的 $Z$ 空间来实现所有可能的二次曲线. (d=2)
$\Phi_2(x)=(1,x_1,x_2,x_1^2,x_1x_2,x_2^2)$
$H_{\Phi_2}=\{h(x):h(x)=\tilde{h}(\Phi_2(x))\ for\ some\ linear\ \tilde{h}\ on\ Z\}$

Nonlinear Transform

Use Nonlinear $\Phi$ + Linear Models to get a Good Quadratic Hypothesis

transform original data $\{(x_n,y_n)\}$ to $\{(z_n=\Phi(x_n),y_n)\}$ by $\Phi$ .

get a good perceptron $\tilde w$ using $\{(z_n,y_n)\}$ and your favorite linear classification algorithm $A$ .

return $g(x)=sign(\tilde w^T\Phi (x))$ .

Price of Nonlinear Transform

以上讨论的是二次可分的情况，最后 $Z$ 空间的维度只有6，但是对于 $Q$ 次的情况我们可以得到 $\binom{Q+d}{d}=O(Q^d)$ 的空间复杂度.

For VC-safety, $\Phi$ shall be decided without ‘peeking’ data .

Structured Hypothesis Sets

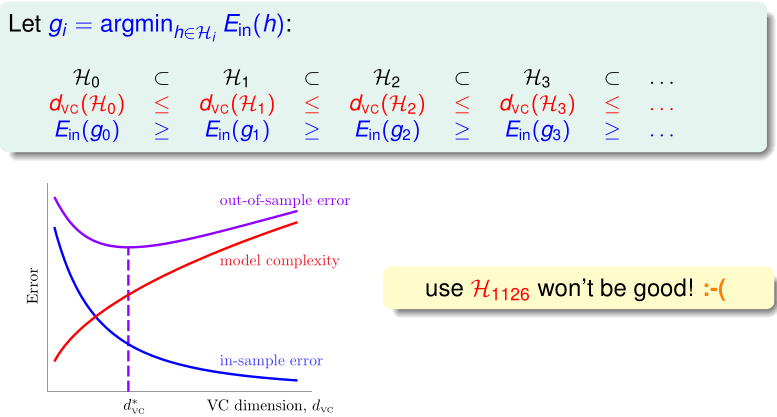
safe route: $H_1$ first
if $E_{in}(g_1)$ good enough, good.
otherwise, move right of the curve with nothing lost except ‘wasted’ computation

linear model first: simple, efficient, safe, and workable !