09-Linear-Regression

Veröffentlicht am

Linear Regresssion Algorithm

use squared error
$E_{in}(w)=\frac{1}{N}\sum_{n=1}^N(w^Tx_n-y_n)^2=\frac{1}{N}\sum_{n=1}^N(x_n^Tw-y_n)^2$
$w\ is\ (d+1)\times1,\ x_n\ is\ (d+1)\times1$
$\Leftrightarrow\frac{1}{N}\left | Xw-Y \right |^2\ with\ X(N,d+1),w(d+1,1),y(N,1)$

$\mathop{min}\limits_wE_{in}(w)=\frac{1}{N}\left | Xw-Y \right |^2$
$E_{in}(w)$ : continuous, differentiable, convex —> necessary condition of ‘best’ w
TASK: find $w_{LIN}$ such that $\bigtriangledown E_{in}(w_{LIN})=0$
$E_{in}(w)=\frac{1}{N}\left | Xw-Y \right |^2=\frac{1}{N}(w^TX^TXw-2w^TX^TY+Y^TY)$
$and\ \bigtriangledown E_{in}(w)=\frac{2}{N}(X^TXw-X^TY)$

  • invertible $X^TX$ —-> unique solution : $w_{LIN}=(X^TX)^{-1}X^TY$ with $X^{‘}=(X^TX)^{-1}X^T$
    ofen the case because $N>>d+1$
  • singular $X^TX$ —-> many optimal solutions, one of the solutions: $w_{LIN}=X^{‘}Y$ by defining $X^{‘}$ in other ways

practical suggestion: use well-implemented $X^{‘}$ instead of $(X^TX)^{-1}X^T$ for numerical stability when almost-singular.

Algorithm :

  • from D, construct input matrix $X(N,d+1)$ and output vector $Y(N,1)$
  • calculate pseudo-inverse $X^{‘}(d+1,N)$
  • return $w_{LIN}(d+1,1)=X^{‘}Y$

Linear Classification vs. Linear Regression

For the efficient analytic solution of LinReg, run LinReg on binary classification data, and return $g(x)=sign(w_{LIN}^Tx)$.

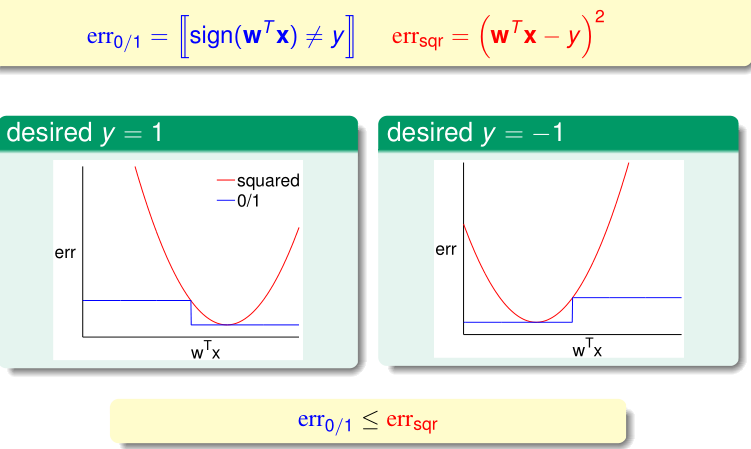
  • (loose) upper bound $err_{sqr}$ as $\hat{err}$ to approximate $err_{0/1}$
  • trade bound tightness for efficiency

$w_{LIN}$ : useful baseline classifier, or as initial PLA/pocket vector.