VC Dimension

$d_{vc}=minimum\ k-1=maximum\ non-breakpoint=d+1$

Step1: prove $d_{vc}\geq d+1$ by shattering some d+1 inputs.
Step2: prove $d_{vc}\leq d+1$ by proving can not shatter any d+2 inputs.

provably & loosely, for $N\geq2,k\geq3$,
$m_H(N)\leq B(N,k)=\sum_{i=0}^{k-1}\binom{N}{i}\leq N^{k-1}$
$BAD\leq 4(2N)^{k-1}exp(…)$
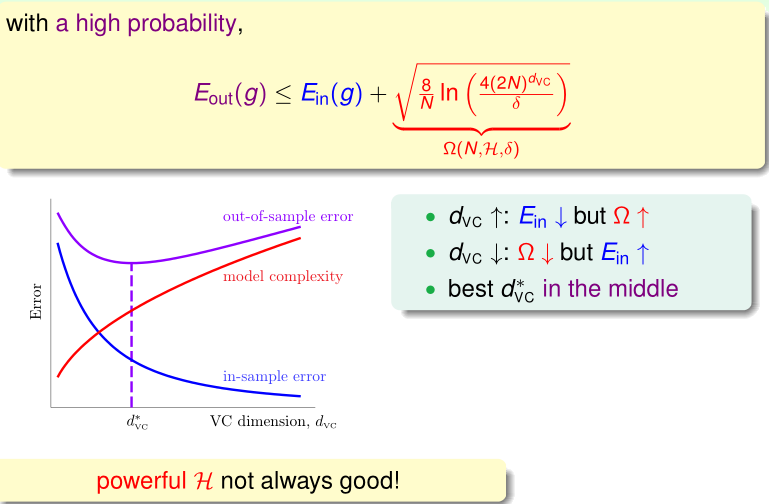
$d_{vc}(H)$: powerfulness of $H$

VC Bound Rephrase: Penalty for Model Complexity

THE VC Message

VC Bound Rephrase: Sample Complexity

Looseness of VC Bound

Noise and Probabilistic Target

如果数据集中包含有噪音，变成对于每一个x，去估计p(y|x)，也就是实际的$Y$变成了f(x)和noise的某种分布.

Error Measure

0/1 error; squared error
err is application/user-dependent

Algorithmic Error Measures $\hat{err}$
true: just err
plausible:
$\qquad \ \ $ 0/1: minimum ‘flipping noise’—NP-hard to optimize
$\qquad \ \ $ squared: minimum Gaussian noise
friendly: easy to optimize for $A$
$\qquad \ \ $ closed-form solution
$\qquad \ \ $ convex objective function

Weighted Pocket Algorithm

当正类被错分为负类的代价较高时，我们设计算法时可以虚拟加大错分样例的比率（实际是增加错分样例的访问概率），算法的其他细节不变.