Trade-off on M
- can we make sure that $E_{out}(g)$ is close enough to $E_{in}(g)$ ?
- can we make $E_{out}(g)$ small enough?
$\mathbb{P}[BAD]\leq 2·M·exp(…)$
对于小的M来说,我们可以做到第一点,但是第二点做不到,因为选择太少了;
对于大的M来说,我们可以做到第二点,但是第一点做不到.
$\mathbb{P}[|E_{in}(g)-E_{out}(g)|>\epsilon]\leq 2·M·exp(-2\epsilon^2N)$
overlapping for similar hypothesis $h_1\approx h_2$
to account for overlapping, we can group similar hypothesis by kind.
lines in 2D
| N |数量(effective(N))|
| :—–:| :—-: |
| 1 | 2 |
| 2| 4 |
| 3 | 8 |
|4|$14<2^N$|
we can replace M by effective(N)
Effective Number of Hypothesis
$h(x_1,x_2,…,x_N)$ called a dichotomy: hypothesis ‘limited’ to the eyes of $x_1,x_2,…,x_N$
$h(x_1,x_2,…,x_N)$ all dichotomies ‘implemented’ by $H$ on $x_1,x_2,…,x_N$ with upper bounded by $2^N$
仅对每一个在数据集上的不同划分进行计数,不同的假设
Growth Function: remove dependence by taking max of all possible $(x_1,x_2,…,x_N)$
$m_H(N)=\mathop{max}\limits_{x_1,x_2,…,x_N\epsilon \chi}|H(x_1,x_2,…,x_N)|$
- positive rays : $\qquad \qquad m_H(N)=N+1$
- positive intervals : $\qquad\ \ m_H(N)=0.5·N^2+0.5·N+1$
- convex sets : $\qquad\qquad\ \ m_H(N)=2^N$
- 2D perceptrons : $\qquad\ \ \ \ m_H(N)<2^N\ in\ some\ cases$
Break Point: if no k inputs can be shattered by $H$, call k a break point for $H$. Will foucus on minimum break point k.
- positive rays : $O(N)$ break point at 2
- positive intervals : $O(N^2)$ break point at 3
- convex sets : $O(2^N)$ no break point
- 2D perceptrons : break point at 4
推论:$m_H(N)=O(N^{k-1})$
Restriction of Break Point
e.g. 当minimum break point k=2时,在N=3时,maximum possible=4<<$2^3$
—>break point k restricts maximum possible $m_H(N)$ a lot for $N>k$
idea: $m_H(N) \leq\ maximum\ possible\ m_H(N)\ given\ k \ \ \leq\ poly(N)$
Bounding Function
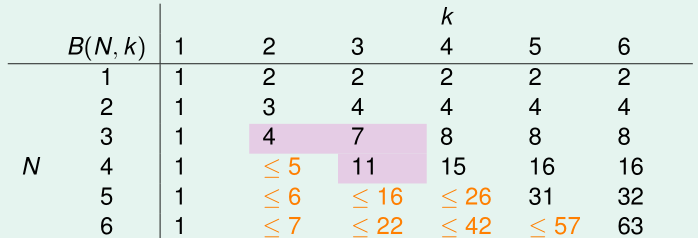
$B(N,K)$ : maximum possible $m_H(N)$ when break point = k
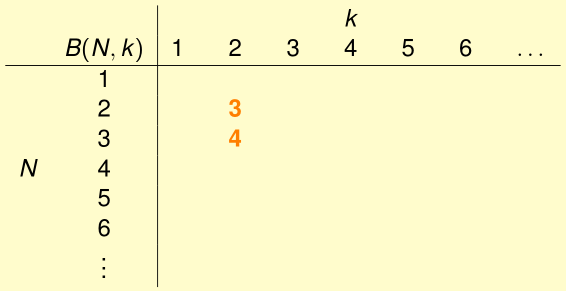
Table of Bounding Function:
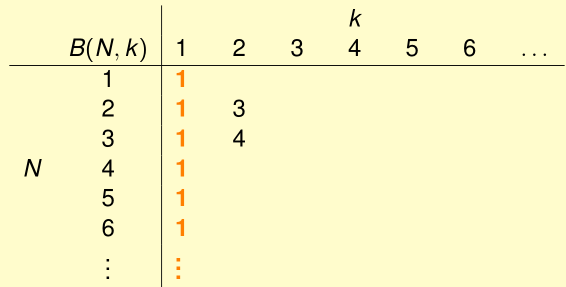
这里我们知道B(2,2)=3; B(3,2)=4
当然B(N,1)=1
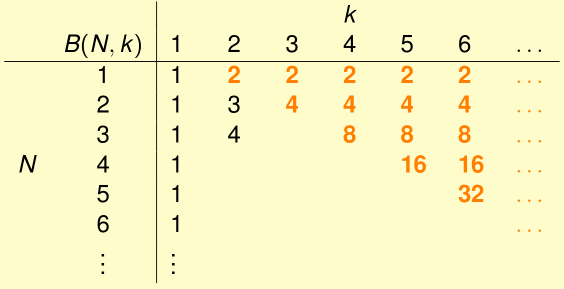
这里当$N<k,\ B(N,k)=2^N$
当$N=k,\ B(N,k)=2^N-1$
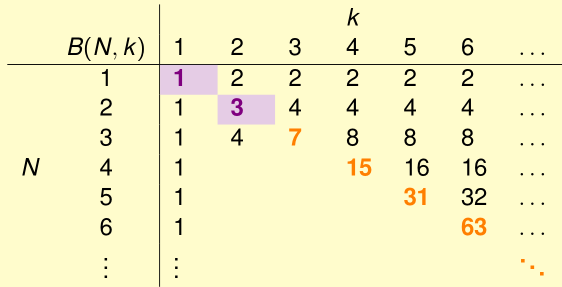
$B(N,k)\leq B(N-1,k)+B(N-1,k-1)$Bounding Function: The Theorem
$B(N,k)\leq \sum_{i=0}^{k-1}\binom{N}{i}$
右边最高项是$N^{k-1}\Rightarrow m_H(N)\ is\ poly(N)\ if\ break\ point\ exists$.
$’\leq’\ can\ be\ ‘=’\ actually$.
Replace M by $m_H(N)$
$M$ 的计数应当是所有可能的 $D$, 而不是 $samples$, 也就是无论 $m_H(N)$ 如何, $N$ 应当是无限的. 如果要替换成关于 $samples$ 的 $N$, 就需要结合 $validation$ 估计 $E_{out}$ 和相应的概率知识作替换.
want: $\mathbb{P}[\exists h\epsilon H\ s.t.\ |E_{in}(h)-E_{out}(h)|>\epsilon]\leq 2·m_H(N)·exp(-2\epsilon^2N)$
from: $\mathbb{P}[\exists h\epsilon H\ s.t.\ |E_{in}(h)-E_{out}(h)|>\epsilon]\leq 2·M·exp(-2\epsilon^2N)$
但我们不能够直接这么做,因为原始式子中|H|是无限的,$E_{out}(h)$是无限的,之前所讨论的是基于采样的in-sample N. 所以为了替换成功我们还需要作些推导.
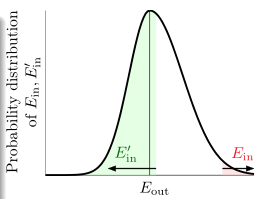
Step1: Replace $E_{out}\ by\ E_{in}^{‘}$, i.e. sample verification set $D’$ of size N to caculate $E_{in}^{‘}$
$\frac {1}{2}\mathbb{P}[\exists h\epsilon H\ s.t.\ |E_{in}(h)-E_{out}(h)|>\epsilon]\leq \mathbb{P}[\exists h\epsilon H\ s.t.\ |E_{in}(h)-E_{in}^{‘}(h)|>\frac {\epsilon}{2}]$
对于上式,基于从$E_{out}$ 到 $E_{in}^{‘}$ 的替换,第一个1/2表示替换之后式子中差值的绝对值大于误差值的概率增加了一倍;第二个1/2表示更加严格的误差限制(数学需要?).Step2: Decompose $H$ by Kind
$BAD\leq 2\mathbb{P}[\exists h\epsilon H\ s.t.\ |E_{in}(h)-E_{in}^{‘}(h)|>\frac {\epsilon}{2}]\\
\qquad\ \leq 2m_H(N)\mathbb{P}[fixed\ h\ s.t.\ |E_{in}(h)-E_{in}^{‘}(h)|>\frac {\epsilon}{2}]$
$E_{in}(h)$ 有 N 笔数据,$E_{in}^{‘}(h)$ 也有 N 笔不同的数据,无限的 $H$ 变成了$|H(x_1,…,x_N,x_1^{‘},…,x_N^{‘})|$,这样我们终于可以使用$m_H(2N)$来计算BAD-overlap了.Step3: Use Hoeffding without Replacement
$BAD \leq 2m_H(N)\mathbb{P}[fixed\ h\ s.t.\ |E_{in}(h)-E_{in}^{‘}(h)|>\frac {\epsilon}{2}]\\
\qquad\ =2m_H(N)\mathbb{P}[fixed\ h\ s.t.\ |E_{in}(h)-\frac{E_{in}+E_{in}^{‘}(h)}{2}|>\frac {\epsilon}{4}]\\
\qquad\ \leq 2m_H(N)·2exp(-2(\frac{\epsilon}{4})^2N)$
其中的代换是很有必要的,因为比较第一次sample与两次sample平均的$E$是使用Hoeffding的条件.
Vapnik-Chervonenkis (VC) bound:
$\mathbb{P}[\exists h\epsilon H\ s.t.\ |E_{in}(h)-E_{out}(h)|>\epsilon]\leq 4m_H(2N)·exp(-\frac{\epsilon^2}{8}N)$