Hoeffding’s Inequality

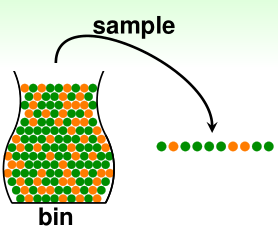
bin: 假设橘色的概率=$\mu$，绿色的概率则是$1-\mu$，这里我们并不知道$\mu$
sample: 独立抽样N个弹珠，其中橘色比率=$v$，那么绿色比率=$1-v$，这里我们知道$v$
in-sample $v$ 能够告诉我们关于 out-of-sample $\mu$ 的信息.

in big sample (N large), $v$ is probably close to $\mu$ (within $\epsilon$):
$\mathbb{P}[|v-\mu|>\epsilon]\leq 2exp(-2\epsilon^2N)$
the statement ‘$v=\mu$’ is probably approximately correct(PAC).

—>Connection to Learning

fixed hypothesis $h(x)=target\ f(x)$ ?
橘色表示$h$犯错了，也就是$h(x)\neq f(x)$
绿色表示$h$是对的，也就是$h(x)= f(x)$
在$D={(x_n,y_n)}$上检验$h$，这里 $x_n$ 满足 $i.i.d$.

若N足够大的话并且$i.i.d.\ x_n$，可能可以通过$h(x_n)\neq y_n$的比率来推论$h(x_n)\neq f(x_n)$的概率.

for any fixed h, in ‘big’ data (N large),
in-sample error $E_{in}(h)=\frac {1}{N}\sum_{n=1}^N[h(x_n)\neq y_n]$ is probably close to
out-of-sample error $E_{out}(h)=\varepsilon_{x\sim P}[h(x)\neq f(x)]$ (within $\epsilon$)
$\mathbb{P}[|E_{in}(h)-E_{out}(h)|>\epsilon]\leq 2exp(-2\epsilon^2N)$

Connection to Real Learning

BAD sample: $E_{in}$ and $E_{out}$ far away

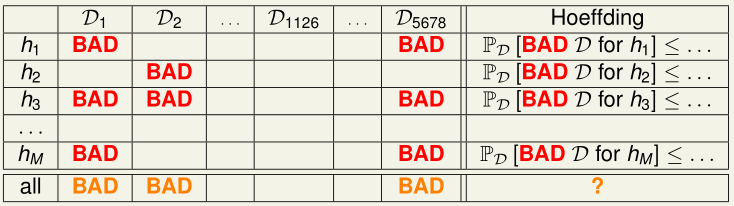
Hoeffding告诉我们对于某个$h\epsilon H,\ E_{in} \ and\ E_{out}$ 相差很大的几率很小，也就是我们遇到BAD sample的几率很小，但是，当我们有选择的时候，也就是如果有多个$h$可以选择，我们可能选到那个$E_{in} \ and\ E_{out}$ 相差很大的$h$的几率会很大(实际上就是 $E_{in}$ 很小，但是 $E_{out} 很大$ )，也就是我们遇到BAD Sample的几率很大.
$\mathbb{P}[BAD\ D]=\sum\limits_{all\ possibleD}\mathbb{P}(D)·[BAD\ D]$ small.

对于很多 $h$ 来说，BAD data 就是只要存在某个 $h$ 在该数据集上$E_{in}$ and $E_{out}$ far away.

Bound of BAD Data
$
\begin{eqnarray}
&&\mathbb{P}_D[BAD\ D]\\
&=&\mathbb{P}_D[BAD\ D\ for\ h_1\ or\ BAD\ D\ for\ h_2\ or\ …\ or\ BAD\ D\ for\ h_M]\\
&\leq& \mathbb{P}_D[BAD\ D\ for\ h_1]+\mathbb{P}_D[BAD\ D\ for\ h_2]+…+\mathbb{P}_D[BAD\ D\ for\ h_M]\\
&\leq&2exp(-2\epsilon^2N)+2exp(-2\epsilon^2N)+…+2exp(-2\epsilon^2N)\\
&=&2Mexp(-2\epsilon^2N)
\end{eqnarray}
$
如果 $|H|=M$ 有限，而N足够大，不管 $A$ 选择什么 $g$，$E_{in}$ and $E_{out}$会大致一样；
如果 $A$ 找到某个 $g$ 使得 $E_{in}$很小，那么 $E_{out}$ 也会很小.

但是实际上总是 $|H|=\infty$