Perceptron Hypothesis Set
- For $x=(x_1,x_2,…,x_d)$ ‘features of customer’, compute a weighted ‘score’ and:
$\quad \quad \quad$ approve credit if $\quad \sum_{i=1}^{d}{w_ix_i} > threshold$
$\quad \quad \quad \quad \ $ deny credit if $\quad \sum_{i=1}^{d}{w_ix_i} < threshold$ - $y$: {+1(good), -1(bad)}, linear formula $h \epsilon H$ are:
$\quad \quad \quad$ $h(x)=sign((\sum_{i=1}^{d}{w_ix_i})-threshold)$ - Vector form:
$
\begin{eqnarray}
h(x) &=& sign((\sum_{i=1}^{d}{w_ix_i})-threshold)\\
&=&sign((\sum_{i=1}^{d}{w_ix_i})+(-threshold)·(+1))\\
&=&sign(\sum_{i=0}^{d}{w_ix_i})\\
&=&sign(w^Tx)
\end{eqnarray}
$
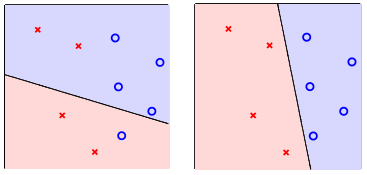
Perceptrons in $R^2$: $h(x)=sign(w_0+w_1x_1+w_2x_2)$
- customer features $x$: points on the plane (or points in $R^d$)
- lables $y$: 。(+1), x(-1)
- hypothesis $h$: lines(or hyperplanes in $R^d$)
- different line classifies customers differently
perceptrons $\Leftrightarrow$linear (binary) classifiers
Percepton Learning Algorithm
Select $g$ from $H$, where $H$=all possible perceptrons.
- want: $g\approx f$ on $D$, ideally $g(x_n)=f(x_n)=y_n$
- diffcult: $H$ is of infinite size
- idea: start from some $g_0$, and ‘correct’ its mistakes on $D$
in PLA, we can represent $g_0$ by its weight vector $w_0$.
For t = 0,1,…
$\quad$find the next mistake of $w_t$ called $(x_{n(t)}, y_{n(t)})$
$\quad\quad\quad\quad sign(w_t^Tx_{n(t)})\neq y_{n(t)}$
$\quad$(try to) correct the mistake by
$\quad\quad\quad\quad w_{t+1}\leftarrow w_t+y_{n(t)}x_{n(t)}$
… until a full cycle of not encountering mistakes
return last $w$ (called $w_{PLA}$) as $g$
(next can follow naive cycle(1,…,N) or precomputed random cycle)
Guarantee of PLA
if(linear separable), after ‘enough’ corrections, any PLA variant halts.
PLA Fact: $w_t$ Gets More Aligned with $w_f$
linear separable $D\ \Leftrightarrow$ exists perfect $w_f$ such that $y_n=sign(w_f^Tx_n)$
- $w_f$ perfect hence every $x_n$ correctly away from line:
$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad y_{n(t)}w_f^Tx_{n(t)}\geqslant \mathop{min}\limits_ny_nw_f^Tx_n>0$ - $w_f^Tw_t\uparrow$ by updating with any $(x_{n(t)},y_{n(t)})$
$
\begin{eqnarray}
w_f^Tw_{t+1}&=&w_f^T(w_t+y_{n(t)}x_{n(t)})\\
&\geq&w_f^Tw_t+\mathop{min}\limits_ny_nw_f^Tx_n\\
&>&w_f^Tw_t+0
\end{eqnarray}
$
$w_t$ appears more aligned with $w_f$ after update.
PLA Fact: $w_t$ Does not Grow too Fast
$w_t$ changed only when mistake $\Leftrightarrow sign(w_f^Tx_{n(t)})\neq y_{n(t)}\Leftrightarrow y_{n(t)}w_f^Tx_{n(t)}\leqslant 0$
- mistake ‘limits’ $|w_t|^2$ growth, even when updating with ‘longest’ $x_n$
$
\begin{eqnarray}
|w_{t+1}|^2&=&|w_t+y_{n(t)}x_{n(t)}|^2\\
&=&|w_t|^2+2y_{n(t)}w_t^Tx_{n(t)}+|y_{n(t)}x_{n(t)}|^2\\
&\leq&|w_t|^2+0+|y_{n(t)}x_{n(t)}|^2\\
&\leq&|w_t|^2+\mathop{max}\limits_n|y_nx_n|^2
\end{eqnarray}
$
start from $w_0=0$, after $T$ mistake corrections:
$\frac {w_f^T}{|w_f|} \frac {w_T}{|w_T|} \geq \sqrt{T}·constant$
PLA告诉我们只要线性可分并且通过错误修正,那么PLA会停下来. 这里PLA实现简单,而且适用于任何维度$d$.
问题在于我们不知道是否$D$线性可分,并且不确定到停止需要多长时间(虽然实际上很快).
Non-Separable Data(Learning with Noisy data)
- assume ‘little’ noise: $y_n=f(x_n)$ usually
- if so, $g\approx f$ on $D\Leftrightarrow y_n=g(x_n)$ usually
- how about
$w_g\leftarrow \mathop{argmin}\limits_w \sum_{n=1}^N [y_n\neq sign(w^Tx_n)]$
——NP-hard to solve, unfortunately.
Pocket Algorithm: modify PLA algorithm (black lines) by keeping best weights in pocket
initialize pocket weights $\hat{w}$
For t=0,1,…
$\quad\quad$find a (random) mistake of $w_t$ called $(x_{n(t)}, y_{n(t)})$
$\quad\quad$(try to) correct the mistake by
$\quad\quad\quad\quad w_{t+1}\leftarrow w_t+y_{n(t)}x_{n(t)}$
$\quad\quad$if $w_{t+1}$ makes fewer mistakes than $\hat{w}$, replace $\hat{w}$ by $w_{t+1}$
…until enough iterations
return $\hat{w}$ (called $w_{POCKET}$) as $g$